Thống kê nghe có vẻ khô khan, nhưng đằng sau những con số là cả một câu chuyện thú vị. Một trong những "nhân vật" quan trọng nhất trong câu chuyện đó chính là phương sai. Tưởng tượng dữ liệu của bạn là một đám đông, phương sai chính là thước đo xem đám đông đó đứng sát nhau hay tản mác khắp nơi so với người "đại diện" là giá trị trung bình. Từ định nghĩa cơ bản nhất, cách "bắt" nó bằng công thức cho từng loại dữ liệu, cho đến ý nghĩa thực sự nó mang lại trong đủ mọi lĩnh vực, và cả mối liên hệ "anh em" với độ lệch chuẩn nữa – phương sai hé lộ rất nhiều điều. Cứ nghĩ đến giá cổ phiếu nhảy múa mỗi ngày, hay điểm thi của cả lớp lúc cao lúc thấp – phương sai chính là thứ giúp chúng ta lượng hóa sự "nhảy múa" hay "lúc cao lúc thấp" đó một cách khách quan. Vậy làm sao để tính toán chính xác, và con số phương sai ấy thực sự nói lên điều gì về tập dữ liệu mà bạn đang quan tâm?
Phương sai là gì Khái niệm đơn giản nhất
Khi chúng ta nhìn vào một tập hợp các con số, việc tính trung bình thôi chưa đủ để hiểu hết về chúng. Trung bình chỉ cho biết "điểm giữa" của dữ liệu, nhưng không nói lên được các con số đó phân bố như thế nào – chúng có tụ lại gần nhau không, hay lại "rải rác" khắp nơi? Đó chính là lúc khái niệm phương sai xuất hiện, như một thước đo đắc lực giúp chúng ta nhìn rõ hơn bức tranh toàn cảnh.
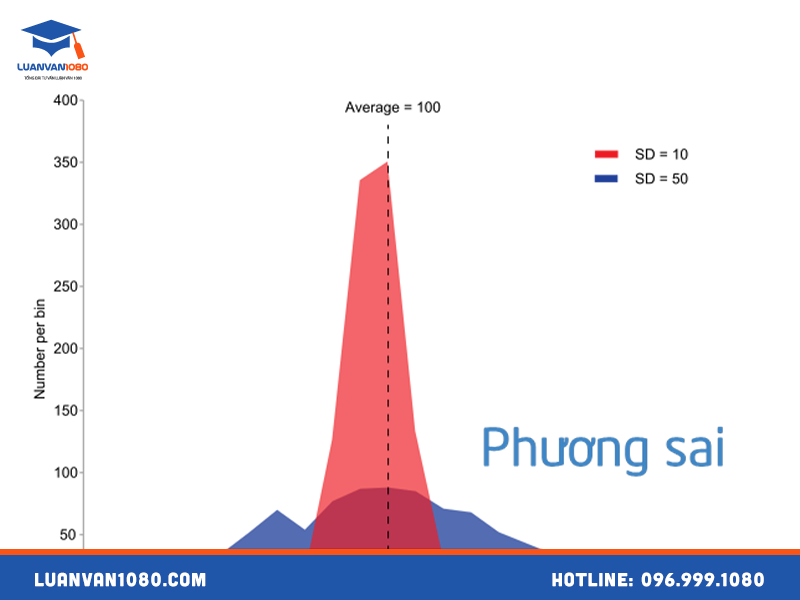
Nói một cách dễ hiểu nhất, phương sai là một con số cho chúng ta biết mức độ phân tán của các điểm dữ liệu so với giá trị trung bình của chúng. Tưởng tượng bạn có điểm thi của một lớp học. Nếu phương sai nhỏ, nghĩa là hầu hết học sinh có điểm gần với điểm trung bình của lớp. Ngược lại, nếu phương sai lớn, điều đó cho thấy điểm số rất đa dạng, có cả người điểm rất cao và người điểm rất thấp, cách xa điểm trung bình.
Về mặt kỹ thuật hơn một chút, phương sai được định nghĩa là trung bình của bình phương độ lệch của từng điểm dữ liệu so với giá trị trung bình. Nghe có vẻ hơi "hàn lâm" nhỉ? Đừng lo, chúng ta sẽ làm rõ nó.
Tại sao lại là "bình phương độ lệch"? À, nếu chỉ lấy độ lệch đơn thuần (giá trị trừ trung bình), thì những giá trị nhỏ hơn trung bình sẽ cho kết quả âm, còn lớn hơn thì dương. Cộng hết lại có khi lại ra gần bằng 0, chẳng nói lên được gì về sự phân tán cả. Việc bình phương giúp loại bỏ dấu âm, đồng thời nhấn mạnh sự khác biệt lớn hơn – những điểm dữ liệu càng xa trung bình thì khi bình phương lên, đóng góp vào phương sai càng nhiều.
Chính vì thế, phương sai đóng vai trò cực kỳ quan trọng trong việc đánh giá mức độ biến động và sự đồng nhất của một tập dữ liệu. Một phương sai lớn chỉ ra rằng dữ liệu có độ biến động cao, kém đồng nhất. Ngược lại, phương sai nhỏ cho thấy dữ liệu khá ổn định, các giá trị tương đồng nhau. Nắm vững khái niệm này là bước đệm vững chắc để đi sâu hơn vào thế giới thống kê và phân tích dữ liệu đấy.
Công thức tính phương sai chi tiết theo từng kiểu dữ liệu
Khi bắt tay vào tính toán phương sai, bạn sẽ thấy công thức có chút khác biệt tùy vào cách dữ liệu được trình bày và liệu chúng ta đang nói về toàn bộ "dân số" (tổng thể) hay chỉ một "lát cắt" nhỏ (mẫu). Hiểu rõ từng công thức giúp bạn áp dụng chính xác và có được cái nhìn đúng đắn nhất về sự phân tán của dữ liệu.
Dữ liệu thô đơn giản
Đây là trường hợp cơ bản nhất, khi bạn có một danh sách các giá trị riêng lẻ.
-
Đối với tổng thể (Population Variance – \(\sigma^2\)): Nếu bạn có dữ liệu của toàn bộ tổng thể, công thức sẽ là:
\(\sigma^2 = \frac{\sum (x_i – \mu)^2}{N}\)
Trong đó:
- \(\sigma^2\) là ký hiệu phương sai của tổng thể.
- \(x_i\) là từng giá trị dữ liệu trong tập hợp.
- \(\mu\) (muy) là giá trị trung bình của tổng thể.
- \(\sum\) là ký hiệu tổng (tổng tất cả các giá trị).
- \(N\) là tổng số phần tử trong tổng thể.
Hiểu nôm na, công thức này tính tổng bình phương khoảng cách từ mỗi điểm dữ liệu đến giá trị trung bình, rồi chia cho tổng số điểm dữ liệu.
-
Đối với mẫu (Sample Variance – \(s^2\)): Khi bạn chỉ có dữ liệu từ một mẫu nhỏ được lấy từ tổng thể lớn hơn, chúng ta dùng công thức khác một chút để ước lượng phương sai của tổng thể:
\(s^2 = \frac{\sum (x_i – \bar{x})^2}{n-1}\)
Trong đó:
- \(s^2\) là ký hiệu phương sai của mẫu.
- \(x_i\) là từng giá trị dữ liệu trong mẫu.
- \(\bar{x}\) (x-bar) là giá trị trung bình của mẫu.
- \(\sum\) là ký hiệu tổng.
- \(n\) là tổng số phần tử trong mẫu.
Tại sao lại chia cho \(n-1\) thay vì \(n\)? Đây là một mẹo nhỏ trong thống kê gọi là "hiệu chỉnh Bessel". Việc chia cho \(n-1\) giúp phương sai mẫu trở thành một ước lượng không chệch (unbiased estimator) cho phương sai tổng thể. Nói cách khác, nó giúp kết quả tính toán từ mẫu "tiệm cận" gần hơn với giá trị thực của tổng thể mà chúng ta không biết hết.
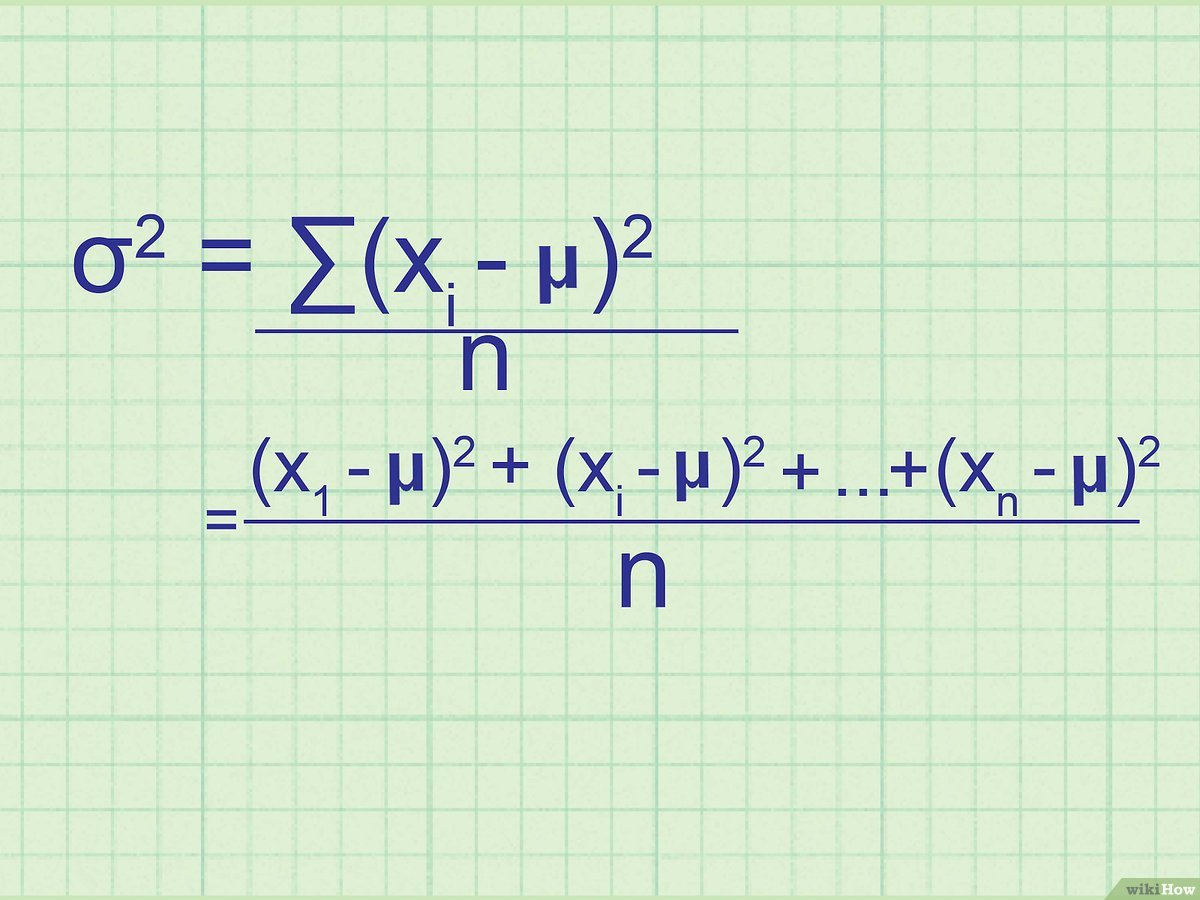
Hiệu chỉnh Bessel trong phương sai
Dữ liệu trong bảng tần số
Khi dữ liệu được trình bày dưới dạng bảng tần số, tức là mỗi giá trị \(x_i\) xuất hiện với một tần số \(f_i\) nhất định, công thức sẽ cần nhân thêm tần số đó vào.
-
Đối với tổng thể (\(\sigma^2\)):
\(\sigma^2 = \frac{\sum f_i (x_i – \mu)^2}{N}\)
Trong đó:
- \(f_i\) là tần số xuất hiện của giá trị \(x_i\).
- \(N = \sum f_i\) là tổng số phần tử trong tổng thể (tổng tất cả các tần số).
- Các ký hiệu khác tương tự như trên.
Công thức này đơn giản là tổng bình phương độ lệch nhân với số lần xuất hiện của độ lệch đó, rồi chia cho tổng số quan sát.
-
Đối với mẫu (\(s^2\)):
\(s^2 = \frac{\sum f_i (x_i – \bar{x})^2}{n-1}\)
Trong đó:
- \(f_i\) là tần số xuất hiện của giá trị \(x_i\) trong mẫu.
- \(n = \sum f_i\) là tổng số phần tử trong mẫu.
- Các ký hiệu khác tương tự.
Vẫn là hiệu chỉnh \(n-1\) quen thuộc để có ước lượng tốt hơn cho phương sai tổng thể.
Dữ liệu ghép lớp (bảng phân phối tần số ghép lớp)
Đôi khi, dữ liệu được gom lại thành các khoảng (lớp). Trong trường hợp này, chúng ta không biết chính xác giá trị của từng phần tử, mà chỉ biết chúng nằm trong khoảng nào. Để tính phương sai, chúng ta thường sử dụng giá trị trung điểm của mỗi lớp làm đại diện cho tất cả các giá trị trong lớp đó.
-
Đối với tổng thể (\(\sigma^2\)):
\(\sigma^2 = \frac{\sum f_i (m_i – \mu)^2}{N}\)
Trong đó:
- \(m_i\) là giá trị trung điểm của lớp thứ \(i\).
- \(f_i\) là tần số của lớp thứ \(i\).
- \(N = \sum f_i\) là tổng số phần tử trong tổng thể.
- \(\mu\) là giá trị trung bình của tổng thể (thường được tính bằng cách sử dụng trung điểm và tần số: \(\mu \approx \frac{\sum f_i m_i}{N}\)).
Lưu ý, đây là một giá trị xấp xỉ vì chúng ta đang dùng trung điểm để đại diện cho cả một khoảng giá trị.
-
Đối với mẫu (\(s^2\)):
\(s^2 = \frac{\sum f_i (m_i – \bar{x})^2}{n-1}\)
Trong đó:
- \(m_i\) là giá trị trung điểm của lớp thứ \(i\).
- \(f_i\) là tần số của lớp thứ \(i\) trong mẫu.
- \(n = \sum f_i\) là tổng số phần tử trong mẫu.
- \(\bar{x}\) là giá trị trung bình của mẫu (thường được tính bằng cách sử dụng trung điểm và tần số: \(\bar{x} \approx \frac{\sum f_i m_i}{n}\)).
Tương tự, đây cũng là một giá trị xấp xỉ và vẫn áp dụng hiệu chỉnh \(n-1\).
Việc lựa chọn đúng công thức dựa trên loại dữ liệu và mục đích (tính cho tổng thể hay ước lượng từ mẫu) là bước đầu tiên và quan trọng nhất để có được kết quả phương sai đáng tin cậy.
Phương sai nói gì về dữ liệu của bạn
Tưởng tượng bạn có một rổ táo, và bạn đo cân nặng của từng quả. Nếu tất cả các quả táo đều nặng gần như nhau, chúng rất đồng đều. Ngược lại, nếu có quả rất nặng, quả rất nhẹ, chúng phân tán lung tung. Phương sai chính là con số giúp bạn đo lường cái sự "phân tán lung tung" đó. Nó cho biết các giá trị trong tập dữ liệu của bạn đang cách xa giá trị trung bình (trung bình cộng) bao nhiêu, bình quân là thế nào.
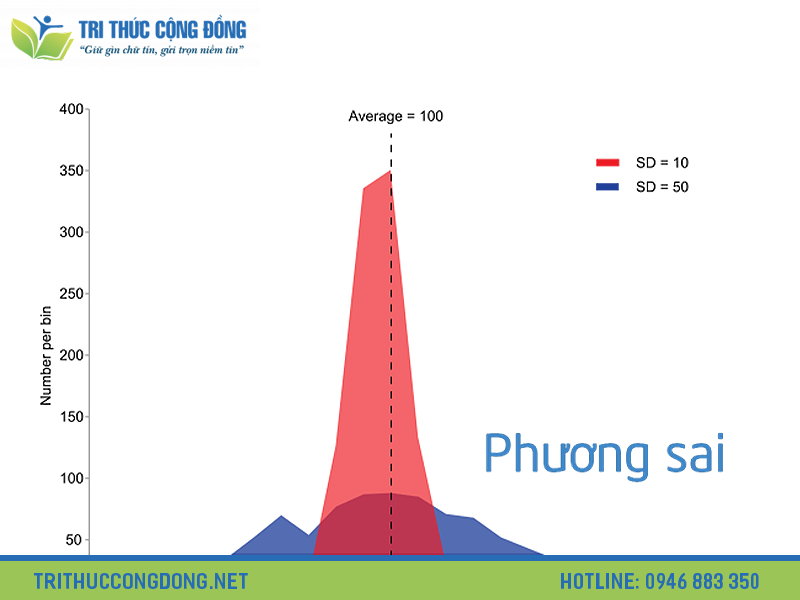
Nói một cách dễ hiểu hơn, phương sai là thước đo sự biến động. Một giá trị phương sai nhỏ cho thấy dữ liệu của bạn tập trung lại gần nhau, quanh giá trị trung bình. Điều này thường ngụ ý tính nhất quán cao. Ví dụ, điểm thi của một lớp có phương sai nhỏ nghĩa là hầu hết học sinh đạt điểm xấp xỉ nhau, không có quá nhiều bạn điểm quá cao hay quá thấp.
Ngược lại, một giá trị phương sai lớn chỉ ra rằng các điểm dữ liệu của bạn trải rộng ra rất xa giá trị trung bình. Dữ liệu biến động mạnh, kém đồng nhất. Trở lại ví dụ điểm thi, phương sai lớn cho thấy điểm số rất phân hóa: có bạn điểm cực cao, có bạn điểm cực thấp, và điểm trung bình có thể không phản ánh đúng bức tranh tổng thể.
Trong phân tích dữ liệu, phương sai đóng vai trò quan trọng như một chỉ báo ban đầu về đặc điểm của tập dữ liệu. Nó giúp chúng ta:
- Đánh giá mức độ rủi ro: Trong tài chính, phương sai của lợi nhuận cổ phiếu thường được dùng để đo lường rủi ro. Phương sai cao nghĩa là lợi nhuận có thể biến động mạnh (lúc lãi nhiều, lúc lỗ nhiều), rủi ro cao hơn.
- So sánh sự ổn định: Khi so sánh hai quy trình sản xuất, quy trình nào cho ra sản phẩm có kích thước với phương sai nhỏ hơn thì thường được coi là ổn định và đáng tin cậy hơn.
- Làm nền tảng cho các phân tích sâu hơn: Phương sai là thành phần cốt lõi trong nhiều kỹ thuật thống kê nâng cao hơn như phân tích phương sai (ANOVA), hồi quy tuyến tính, hay kiểm định giả thuyết.
Tuy nhiên, phương sai cũng có những hạn chế riêng. Điểm trừ lớn nhất là đơn vị của nó bị bình phương so với đơn vị gốc của dữ liệu. Nếu bạn đo chiều cao bằng mét, phương sai sẽ có đơn vị là mét vuông. Điều này khiến việc diễn giải ý nghĩa thực tế của con số phương sai trở nên khó khăn và kém trực quan. Một nhược điểm khác là phương sai rất nhạy cảm với các giá trị ngoại lai (outliers) – những điểm dữ liệu cực đoan có thể kéo giá trị phương sai lên rất cao, làm sai lệch bức tranh về sự phân tán của phần lớn dữ liệu. Dù vậy, không thể phủ nhận vai trò nền tảng của phương sai trong thế giới thống kê và phân tích dữ liệu.
Độ lệch chuẩn và Phương sai Anh em nhà thống kê
Nếu phương sai là "bình phương" của sự phân tán, thì độ lệch chuẩn chính là "căn bậc hai" của phương sai. Nghe có vẻ đơn giản vậy thôi, nhưng chính cái bước lấy căn bậc hai này lại tạo nên sự khác biệt lớn trong cách chúng ta nhìn nhận và diễn giải dữ liệu. Hai anh em này luôn đi cùng nhau, bổ trợ cho nhau, nhưng mỗi người lại có một vai trò riêng trong câu chuyện thống kê.

Mối liên hệ mật thiết
Độ lệch chuẩn, ký hiệu là s (đối với mẫu) hoặc σ (đối với tổng thể), được định nghĩa trực tiếp từ phương sai. Cụ thể, độ lệch chuẩn chính là căn bậc hai không âm của phương sai. Công thức đơn giản là:
- Độ lệch chuẩn = √Phương sai
Điều này có nghĩa là nếu bạn đã tính được phương sai, việc tìm độ lệch chuẩn chỉ là một bước tính toán nhỏ nữa. Chúng đo lường cùng một thứ – mức độ biến động hay phân tán của dữ liệu xung quanh giá trị trung bình – nhưng ở hai "đơn vị" khác nhau.
Khác biệt ở đơn vị và cách diễn giải
Đây là điểm mấu chốt khiến độ lệch chuẩn thường được "ưu ái" hơn trong các báo cáo và phân tích thực tế.
- Phương sai: Đơn vị của phương sai là bình phương đơn vị của dữ liệu gốc. Ví dụ, nếu dữ liệu của bạn là chiều cao tính bằng centimet (cm), thì phương sai sẽ có đơn vị là cm². Nếu dữ liệu là tiền lương tính bằng đồng, phương sai sẽ là đồng². Điều này khiến việc diễn giải con số phương sai trở nên hơi "khó nuốt". Phương sai bằng 100 cm² thì có nghĩa là gì? Nó không trực quan lắm khi so sánh với chiều cao trung bình tính bằng cm.
- Độ lệch chuẩn: Nhờ phép lấy căn bậc hai, độ lệch chuẩn trở lại đơn vị đo lường ban đầu của dữ liệu. Chiều cao tính bằng cm thì độ lệch chuẩn cũng tính bằng cm. Tiền lương tính bằng đồng thì độ lệch chuẩn cũng tính bằng đồng. Điều này giúp chúng ta dễ dàng hình dung và so sánh độ lệch chuẩn với giá trị trung bình. Nếu chiều cao trung bình là 165 cm và độ lệch chuẩn là 7 cm, chúng ta có thể hiểu rằng phần lớn mọi người có chiều cao nằm trong khoảng từ 165 – 7 = 158 cm đến 165 + 7 = 172 cm (đây là một cách diễn giải phổ biến dựa trên quy tắc thực nghiệm, đặc biệt với phân phối chuẩn).
Vì sao độ lệch chuẩn được ưa chuộng hơn?
Chính vì sự "cùng đơn vị" với dữ liệu gốc và giá trị trung bình mà độ lệch chuẩn trở nên thân thiện và dễ hiểu hơn rất nhiều khi trình bày kết quả phân tích.
- Dễ hình dung: Con số độ lệch chuẩn cho chúng ta cảm giác trực quan hơn về mức độ "lệch" điển hình của một điểm dữ liệu so với giá trị trung bình.
- Dễ so sánh: Khi so sánh độ phân tán giữa các tập dữ liệu khác nhau hoặc so sánh độ phân tán với giá trị trung bình, việc sử dụng độ lệch chuẩn giúp việc đối chiếu trở nên ý nghĩa hơn.
- Ứng dụng trong khoảng tin cậy: Độ lệch chuẩn là nền tảng để xây dựng các khoảng tin cậy hay kiểm định giả thuyết, những công cụ quan trọng trong suy luận thống kê.
Tóm lại, phương sai là một bước tính toán quan trọng trên con đường tìm ra độ lệch chuẩn. Nó mang ý nghĩa lý thuyết sâu sắc về sự phân tán, nhưng độ lệch chuẩn mới là "người hùng" khi cần truyền tải thông tin về mức độ biến động một cách rõ ràng, dễ hiểu và trực quan nhất trong thế giới thực.
Phương sai: Từ Số Liệu Đến Thực Tiễn Đời Sống
Thoạt nghe, phương sai có vẻ như một khái niệm khô khan chỉ dành cho giới thống kê hay toán học. Nhưng tin tôi đi, chỉ số này lại xuất hiện và đóng vai trò quan trọng trong rất nhiều khía cạnh của cuộc sống và công việc hàng ngày đấy. Nó giúp chúng ta định lượng được sự "lung lay", sự không chắc chắn hay mức độ phân tán của mọi thứ, từ kết quả thí nghiệm cho đến giá cổ phiếu.
Trong thế giới tài chính, phương sai là một người bạn đồng hành không thể thiếu. Nó được dùng để đo lường rủi ro của một khoản đầu tư. Bạn nghe nói về sự "biến động" của thị trường chứng khoán đúng không? Đó chính là phương sai đang thể hiện vai trò của mình đấy. Một cổ phiếu có phương sai cao thường có giá lên xuống thất thường, hứa hẹn lợi nhuận lớn nhưng cũng đi kèm rủi ro cao hơn. Ngược lại, cổ phiếu phương sai thấp thì ổn định hơn, ít biến động hơn. Các nhà đầu tư dựa vào chỉ số này để cân nhắc xem họ sẵn sàng chấp nhận mức độ rủi ro nào.

Không chỉ có tài chính, ngay cả trong lĩnh vực khoa học và kỹ thuật, phương sai cũng cực kỳ hữu ích. Khi các nhà khoa học thực hiện thí nghiệm, kết quả thường không bao giờ giống hệt nhau. Phương sai giúp họ đo lường sự khác biệt đó, đánh giá độ chính xác của các phép đo hay sự ổn định của một quy trình sản xuất. Trong kiểm soát chất lượng, nếu phương sai của kích thước sản phẩm quá lớn, điều đó báo hiệu có vấn đề trong dây chuyền cần được khắc phục ngay.
Nhìn rộng hơn trong phân tích dữ liệu, phương sai giúp chúng ta hiểu rõ hơn về bản chất của tập dữ liệu đang nghiên cứu. Chẳng hạn, khi khảo sát mức độ hài lòng của khách hàng, phương sai lớn cho thấy ý kiến của mọi người rất khác nhau, có người cực kỳ hài lòng, có người lại rất không hài lòng. Phương sai nhỏ thì ngược lại, đa số mọi người có cùng mức độ hài lòng tương đồng.
Khi làm việc với phương sai, bạn sẽ gặp một vài "biến thể" của nó, tùy thuộc vào dữ liệu bạn có và mục đích phân tích:
- Phương sai tổng thể: Đây là phương sai được tính toán khi bạn có dữ liệu của toàn bộ tập hợp mà bạn quan tâm (tổng thể). Ví dụ, bạn có điểm thi của tất cả học sinh lớp 12 trong một trường.
- Phương sai mẫu: Thực tế, chúng ta hiếm khi có dữ liệu của cả tổng thể. Thường thì chúng ta chỉ thu thập dữ liệu từ một mẫu nhỏ hơn (một nhóm học sinh bất kỳ trong trường). Phương sai mẫu được tính từ dữ liệu mẫu này và dùng để ước lượng phương sai của tổng thể. Công thức tính phương sai mẫu có một chút khác biệt nhỏ (chia cho N-1 thay vì N) để đảm bảo ước lượng này "chuẩn" hơn.
- Phương sai chi phí: Trong quản lý dự án hoặc kế toán quản trị, đây là sự chênh lệch giữa chi phí thực tế đã bỏ ra so với chi phí dự kiến ban đầu. Nó giúp theo dõi xem dự án có đang đi đúng ngân sách hay không.
- Phương sai thặng dư: Khái niệm này thường xuất hiện trong phân tích hồi quy (một kỹ thuật dự đoán). Khi bạn xây dựng một mô hình để dự đoán một giá trị (ví dụ: dự đoán giá nhà dựa trên diện tích), mô hình sẽ đưa ra một giá trị dự đoán. Tuy nhiên, giá nhà thực tế có thể khác. Phương sai thặng dư đo lường sự phân tán của các giá trị thực tế xung quanh đường dự đoán của mô hình. Nó cho biết "phần còn lại" của sự biến động trong dữ liệu mà mô hình chưa giải thích được.
Hiểu được các ứng dụng và phân loại này giúp chúng ta không chỉ biết cách tính phương sai mà còn biết khi nào và làm thế nào để sử dụng nó một cách hiệu quả nhất trong các tình huống thực tế.

