Trong thế giới dữ liệu, không phải lúc nào mọi thứ cũng "đều như vắt chanh". Đôi khi, chúng ta cần biết dữ liệu phân tán hay tập trung như thế nào quanh giá trị trung bình. Tưởng tượng bạn đang so sánh hai cơ hội đầu tư: cả hai đều hứa hẹn lợi nhuận trung bình 10%, nhưng tại sao một cái lại khiến bạn "đau tim" hơn cái kia? Đó chính là lúc chúng ta cần đến một "thước đo" đặc biệt để giải mã sự biến động này. Làm sao để biết tập dữ liệu của bạn đang "ổn định" hay "lộn xộn" một cách khoa học nhất?
Độ lệch chuẩn Là gì và Tại sao cần biết
Khi nói về dữ liệu, không chỉ giá trị trung bình là quan trọng đâu nhé. Tưởng tượng bạn có hai lớp học, điểm trung bình môn Toán đều là 7.5. Nghe có vẻ giống nhau nhỉ? Nhưng nếu ở lớp A, hầu hết học sinh đều đạt điểm quanh quẩn 7.5, còn ở lớp B thì có bạn được 10, có bạn lại chỉ được 5, thậm chí 3? Rõ ràng, dù trung bình như nhau, cách phân bố điểm của hai lớp này lại khác một trời một vực.
Đây chính là lúc độ lệch chuẩn bước ra sân khấu. Đơn giản mà nói, độ lệch chuẩn là một con số cho chúng ta biết dữ liệu trong một tập hợp "tụm lại" hay "tản ra" nhiều như thế nào so với giá trị trung bình của nó. Nó là thước đo sự phân tán, sự biến động của dữ liệu. Một độ lệch chuẩn nhỏ cho thấy các điểm dữ liệu nằm gần giá trị trung bình, tức là dữ liệu khá đồng nhất, ít biến động. Ngược lại, độ lệch chuẩn lớn báo hiệu dữ liệu phân tán rộng, nhiều điểm nằm xa giá trị trung bình, cho thấy sự biến động cao hơn.
Vậy, bản chất của độ lệch chuẩn là gì? Nó bắt nguồn từ một khái niệm anh em thân thiết là phương sai. Phương sai tính tổng bình phương khoảng cách từ mỗi điểm dữ liệu đến giá trị trung bình, rồi chia cho số lượng điểm (hoặc số lượng điểm trừ 1, tùy thuộc vào đó là tổng thể hay mẫu). Việc bình phương khoảng cách giúp loại bỏ dấu âm và nhấn mạnh những điểm nằm càng xa trung bình.
Tuy nhiên, phương sai lại có một nhược điểm nhỏ: đơn vị của nó là bình phương đơn vị gốc của dữ liệu (ví dụ, nếu dữ liệu là điểm số, phương sai sẽ có đơn vị là "điểm bình phương", hơi khó hiểu). Để đưa thước đo này về cùng đơn vị với dữ liệu gốc và giá trị trung bình, người ta chỉ đơn giản là lấy căn bậc hai của phương sai. Và đó chính là độ lệch chuẩn!
Nói cách khác, độ lệch chuẩn chính là "phiên bản" dễ hiểu hơn của phương sai, giúp chúng ta trực quan hóa mức độ biến động của dữ liệu ngay trên thang đo ban đầu. Nó cho biết, trung bình, các điểm dữ liệu "lệch" khỏi giá trị trung bình khoảng bao nhiêu. Hiểu được độ lệch chuẩn giúp chúng ta nhìn sâu hơn vào cấu trúc của dữ liệu, không chỉ dừng lại ở con số trung bình đơn thuần. Nó là công cụ đắc lực để so sánh mức độ ổn định hoặc rủi ro giữa các tập dữ liệu khác nhau.
Giải mã cách tính độ lệch chuẩn
Hiểu rõ độ lệch chuẩn là gì là bước đầu tiên, nhưng làm sao để biến khái niệm đó thành một con số cụ thể từ tập dữ liệu của bạn? Đây là lúc chúng ta bắt tay vào phần thực hành. Tưởng tượng bạn đang so sánh sự biến động giá của hai loại trái cây trên thị trường, hay đánh giá rủi ro của hai khoản đầu tư khác nhau – con số độ lệch chuẩn chính là thước đo giúp bạn làm điều đó. Vậy, làm thế nào để tính toán chỉ số quan trọng này một cách chính xác nhất, dù bạn muốn tự tay thực hiện hay nhờ cậy công cụ hỗ trợ?
Hai Công thức Tính Độ lệch chuẩn
À, nói đến công thức tính độ lệch chuẩn thì không phải chỉ có một đâu nhé. Tùy vào việc bạn đang nhìn vào toàn bộ cái "tổng thể" mà mình quan tâm, hay chỉ là một phần nhỏ đại diện cho nó (gọi là "mẫu"), mà công thức sẽ có chút khác biệt.
Đầu tiên là công thức cho tổng thể – tức là khi bạn có dữ liệu của tất tần tật mọi thứ bạn muốn nghiên cứu. Công thức này dùng ký hiệu σ (đọc là sigma) để chỉ độ lệch chuẩn. Nó trông như thế này nè:
σ = √[ Σ(xi – μ)² / N ]
Trong đó:
- σ: Chính là độ lệch chuẩn của tổng thể mà chúng ta đang tìm.
- Σ: Ký hiệu tổng, nghĩa là bạn phải cộng tất cả các giá trị sau nó lại.
- xi: Là từng giá trị dữ liệu riêng lẻ trong tổng thể.
- μ (đọc là mu): Là giá trị trung bình của toàn bộ tổng thể.
- N: Là tổng số phần tử, hay kích thước của tổng thể.
Còn khi bạn chỉ có một mẫu – một nhóm nhỏ được chọn ra từ tổng thể lớn hơn – thì chúng ta dùng công thức khác một chút. Độ lệch chuẩn của mẫu được ký hiệu là s. Công thức của em nó đây:
s = √[ Σ(xi – x̄)² / (n – 1) ]
Nhìn qua thì giống công thức trên nhỉ? Nhưng để ý kỹ nè:
- s: Là độ lệch chuẩn của mẫu.
- Σ: Vẫn là ký hiệu tổng.
- xi: Vẫn là từng giá trị dữ liệu, nhưng là trong mẫu.
- x̄ (đọc là x gạch ngang): Là giá trị trung bình của mẫu.
- n: Là kích thước của mẫu (số lượng phần tử trong mẫu).
Điểm khác biệt lớn nhất nằm ở chỗ mẫu số: thay vì chia cho N (kích thước tổng thể), chúng ta lại chia cho n-1.
Tại sao lại là n-1 mà không phải n? À, đây là một kỹ thuật nhỏ trong thống kê gọi là hiệu chỉnh Bessel. Chia cho n-1 giúp cho độ lệch chuẩn của mẫu (s) trở thành một ước lượng ít chệch (unbiased estimate) tốt hơn cho độ lệch chuẩn thực sự của tổng thể (σ). Nghe hơi hàn lâm tí, nhưng hiểu đơn giản là nó giúp kết quả tính từ mẫu "gần" với kết quả thật của tổng thể hơn, đặc biệt là khi kích thước mẫu n còn nhỏ.
Vậy là rõ rồi nhé. Khi làm việc với toàn bộ dữ liệu của nhóm mình quan tâm, dùng công thức với σ và chia cho N. Còn khi chỉ có dữ liệu của một mẫu đại diện, dùng công thức với s và chia cho n-1. Nhớ kỹ hai ký hiệu và mẫu số này là bạn đã nắm được chìa khóa rồi đó!

Tự tay tính độ lệch chuẩn chi tiết từng bước
Đôi khi, để thực sự "thấm" một khái niệm, không gì bằng việc tự mình xắn tay áo lên làm thử. Tính độ lệch chuẩn thủ công nghe có vẻ hơi "cổ điển" trong thời đại máy tính, nhưng nó giúp bạn hiểu rõ từng mảnh ghép tạo nên con số đó. Nào, cùng thử với một ví dụ nhỏ nhé!
Giả sử chúng ta có một tập dữ liệu đơn giản gồm các số sau: 2, 4, 4, 5, 6, 8. Có tất cả 6 số trong tập này.
Bước 1: Tìm số trung bình cộng
Đây là bước đầu tiên và quen thuộc nhất. Bạn chỉ việc cộng tất cả các số lại rồi chia cho tổng số lượng các số.
Tổng các số là: 2 + 4 + 4 + 5 + 6 + 8 = 29
Số lượng các số là: 6
Trung bình cộng (ký hiệu là \(\bar{x}\) nếu là mẫu, hoặc \(\mu\) nếu là tổng thể) sẽ là: 29 / 6 ≈ 4.83
Bước 2: Tính khoảng cách từ mỗi số đến số trung bình
Bây giờ, lấy từng số trong tập dữ liệu ban đầu trừ đi số trung bình vừa tính. Kết quả này cho biết mỗi điểm dữ liệu "lệch" bao nhiêu so với giá trị trung tâm.
- 2 – 4.83 = -2.83
- 4 – 4.83 = -0.83
- 4 – 4.83 = -0.83
- 5 – 4.83 = 0.17
- 6 – 4.83 = 1.17
- 8 – 4.83 = 3.17
Bạn sẽ thấy có cả số âm và số dương ở đây.
Bước 3: Bình phương từng khoảng cách đó
Để loại bỏ dấu âm và làm nổi bật sự chênh lệch lớn, chúng ta sẽ bình phương (nhân với chính nó) từng kết quả ở Bước 2.
- (-2.83)² ≈ 8.01
- (-0.83)² ≈ 0.69
- (-0.83)² ≈ 0.69
- (0.17)² ≈ 0.03
- (1.17)² ≈ 1.37
- (3.17)² ≈ 10.05
Các con số này chính là bình phương độ lệch của mỗi điểm dữ liệu.
Bước 4: Cộng tất cả kết quả bình phương lại
Tiếp theo, hãy cộng tất cả các số bạn vừa tính được ở Bước 3 lại với nhau.
Tổng = 8.01 + 0.69 + 0.69 + 0.03 + 1.37 + 10.05 ≈ 20.84
Tổng này còn được gọi là tổng bình phương độ lệch.
Bước 5: Chia tổng vừa tìm cho số lượng dữ liệu (trừ đi 1 nếu là mẫu)
Đây là bước để tính phương sai. Nếu tập dữ liệu của bạn là toàn bộ tổng thể, bạn sẽ chia tổng ở Bước 4 cho tổng số lượng dữ liệu (N). Nếu tập dữ liệu của bạn chỉ là một mẫu nhỏ được lấy từ tổng thể lớn hơn (trường hợp phổ biến hơn), bạn sẽ chia cho số lượng dữ liệu trừ đi 1 (n-1).
Trong ví dụ này, giả sử đây là một mẫu dữ liệu, số lượng dữ liệu là 6 (n=6). Chúng ta sẽ chia cho n-1 = 6-1 = 5.
Phương sai (ký hiệu là s² cho mẫu, hoặc σ² cho tổng thể) ≈ 20.84 / 5 ≈ 4.17
Bước 6: Lấy căn bậc hai của kết quả cuối cùng
Cuối cùng, để quay trở lại đơn vị đo lường ban đầu (vì chúng ta đã bình phương ở Bước 3), hãy lấy căn bậc hai của phương sai vừa tính.
Độ lệch chuẩn (ký hiệu là s cho mẫu, hoặc σ cho tổng thể) = √Phương sai ≈ √4.17 ≈ 2.04
Vậy là xong! Với tập dữ liệu nhỏ bé ban đầu, độ lệch chuẩn (mẫu) của chúng ta xấp xỉ 2.04. Con số này cho ta biết mức độ phân tán trung bình của các điểm dữ liệu so với giá trị trung bình là khoảng 2.04 đơn vị.
Tính Độ Lệch Chuẩn Nhanh Gọn Với Công Cụ Hỗ Trợ
Sau khi đã hiểu công thức và cách tính thủ công, bạn sẽ thấy việc này hơi mất thời gian nếu dữ liệu nhiều. May mắn thay, chúng ta có những công cụ cực mạnh giúp tính độ lệch chuẩn chỉ trong nháy mắt. Excel và máy tính Casio là hai người bạn đồng hành tuyệt vời đấy!
Tính trên Excel
Excel có sẵn hàm tính độ lệch chuẩn siêu tiện lợi. Bạn chỉ cần biết dùng hàm nào cho đúng thôi.
STDEV.P(range): Dùng khi tập dữ liệu của bạn là toàn bộ tổng thể. Chữ P là viết tắt của Population đấy.STDEV.S(range): Dùng khi tập dữ liệu của bạn chỉ là một mẫu được lấy từ tổng thể lớn hơn. Chữ S là Sample.
Cách dùng:
- Nhập dữ liệu của bạn vào một cột hoặc một hàng trong bảng tính.
- Chọn một ô trống bất kỳ nơi bạn muốn hiển thị kết quả.
- Gõ dấu bằng (=) rồi nhập tên hàm bạn cần (
STDEV.PhoặcSTDEV.S). - Mở ngoặc đơn
(. - Bôi đen vùng dữ liệu chứa các số bạn muốn tính (ví dụ: A1:A10).
- Đóng ngoặc đơn
). - Nhấn Enter. Kết quả sẽ hiện ra ngay lập tức.
Ví dụ, nếu dữ liệu của bạn từ ô A1 đến A10, bạn chỉ cần gõ =STDEV.S(A1:A10) hoặc =STDEV.P(A1:A10). Đơn giản phải không nào?
Tính bằng Máy Tính Casio
Chiếc máy tính Casio quen thuộc cũng là một trợ thủ đắc lực. Nó có chế độ thống kê giúp bạn tính toán nhanh lắm.
Các bước cơ bản (có thể khác chút tùy đời máy):
- Nhấn
MODE(hoặcSETUP). - Tìm và chọn chế độ
STAT(Thống kê). Thường là số 3 hoặc 6. - Chọn loại tính toán thống kê 1 biến (1-VAR). Thường là số 1.
- Màn hình sẽ hiện bảng để bạn nhập dữ liệu. Nhập từng số rồi nhấn
=để xuống dòng. - Nhập xong, nhấn
AC(hoặcON) để thoát khỏi chế độ nhập dữ liệu (dữ liệu vẫn lưu). - Bây giờ là lúc lấy kết quả. Nhấn
SHIFTrồi nhấn phím1(hoặc phím có chữ STAT ở trên). - Chọn mục
Var(Biến). Thường là số 4. - Bạn sẽ thấy các ký hiệu thống kê. Tìm:
σx: Độ lệch chuẩn cho tổng thể.sx: Độ lệch chuẩn cho mẫu.
- Chọn ký hiệu bạn cần (thường là số 3 cho
σxhoặc số 4 chosx), nhấn=, và kết quả sẽ hiện ra.
Tính bằng máy tính vừa nhanh vừa gọn, rất tiện cho lúc đi thi hoặc cần kết quả tức thời.
Tóm lại, dù là Excel hay máy tính Casio, cả hai đều giúp bạn tiết kiệm kha khá thời gian và công sức khi tính độ lệch chuẩn, đặc biệt với bộ dữ liệu lớn. Nắm vững cách dùng các công cụ này sẽ giúp bạn làm việc với số liệu hiệu quả hơn nhiều đấy!
Độ lệch chuẩn Nói gì về Dữ liệu của Bạn
Khi bạn đã tính toán ra con số độ lệch chuẩn, nó không chỉ là một con số khô khan đâu nhé. Con số này chính là "tiếng nói" của tập dữ liệu, mách cho bạn biết về mức độ "lộn xộn" hay "ngăn nắp" của chúng.
Hãy hình dung giá trị trung bình như một điểm neo ở giữa. Độ lệch chuẩn cho bạn biết các điểm dữ liệu còn lại đang "neo đậu" gần hay xa cái điểm giữa đó.
Nếu con số độ lệch chuẩn nhỏ, điều đó có nghĩa là hầu hết các điểm dữ liệu đều tụm lại rất sát quanh giá trị trung bình. Dữ liệu của bạn rất tập trung, thể hiện sự nhất quán cao. Mọi thứ khá ổn định, ít biến động.
Ngược lại, nếu độ lệch chuẩn lớn, thì các điểm dữ liệu lại "tản mác" rất xa giá trị trung bình. Dữ liệu của bạn phân tán rộng, cho thấy sự biến động mạnh mẽ. Có thể có những giá trị rất cao và những giá trị rất thấp, tạo nên một bức tranh dữ liệu "loãng" hơn.
Hiểu được ý nghĩa này giúp bạn so sánh các tập dữ liệu khác nhau một cách sâu sắc hơn, vượt qua việc chỉ nhìn vào giá trị trung bình. Ví dụ, hai nhóm học sinh có thể có điểm trung bình môn Toán như nhau. Nhưng nếu nhóm A có độ lệch chuẩn nhỏ, nghĩa là điểm của các bạn trong nhóm rất đồng đều, không có ai quá giỏi hay quá yếu so với mặt bằng chung. Còn nhóm B có độ lệch chuẩn lớn, tức là điểm số rất chênh lệch, có thể có vài "thần đồng" nhưng cũng không ít bạn còn đang chật vật.
Tóm lại, độ lệch chuẩn là thước đo "sự lan tỏa" của dữ liệu. Nó giúp bạn nhìn thấy bức tranh toàn cảnh về cách các giá trị phân bố xung quanh trung tâm, từ đó đưa ra những nhận định chính xác hơn về tính chất của tập dữ liệu mà bạn đang xem xét.
Độ lệch chuẩn được dùng như thế nào?
Chúng ta đã cùng tìm hiểu độ lệch chuẩn là gì và cách "giải mã" những con số để tính toán nó. Nhưng biết tính thôi chưa đủ, quan trọng là dùng nó để làm gì trong cuộc sống thực, đúng không nào? Hóa ra, con số tưởng chừng khô khan này lại là một "ngôi sao" thầm lặng, xuất hiện trong rất nhiều lĩnh vực, giúp chúng ta hiểu rõ hơn về thế giới xung quanh. Bạn có bao giờ tự hỏi, khi đầu tư vào cổ phiếu hay quỹ, làm sao để biết mức độ "chông chênh" hay rủi ro của nó không? Độ lệch chuẩn chính là một trong những chỉ số giúp trả lời câu hỏi đó. Hay trong nghiên cứu khoa học, làm sao để đánh giá sự khác biệt hay đồng đều giữa các nhóm dữ liệu? Cùng khám phá xem độ lệch chuẩn đã "phá đảo" thế giới thực như thế nào nhé!
Độ lệch chuẩn Nói gì về Dữ liệu của Bạn
Khi bắt tay vào "giải mã" một tập dữ liệu, chúng ta thường nhìn ngay vào giá trị trung bình. Nhưng chỉ mình "anh chàng" trung bình thôi thì chưa đủ để kể hết câu chuyện đâu nhé. Lúc này, độ lệch chuẩn bước vào sân khấu, đóng vai trò như một người bạn đồng hành cực kỳ quan trọng trong thống kê mô tả.
Nó không chỉ là một con số khô khan, mà là thước đo cho bạn biết dữ liệu của mình "tụ tập" gần nhau hay "tản mác" khắp nơi so với giá trị trung bình. Tưởng tượng thế này: bạn có điểm thi của hai lớp học, cả hai đều có điểm trung bình là 7.0. Nhưng lớp A có độ lệch chuẩn nhỏ (ví dụ 0.5), nghĩa là hầu hết học sinh đều đạt điểm quanh quẩn 6.5 đến 7.5. Còn lớp B có độ lệch chuẩn lớn (ví dụ 2.0), điểm số có thể trải dài từ 5.0 đến 9.0. Rõ ràng, bức tranh về sự đồng đều hay chênh lệch trình độ giữa hai lớp này hoàn toàn khác nhau, và độ lệch chuẩn đã giúp chúng ta nhìn thấy điều đó.
Trong các nghiên cứu khoa học, từ y học, xã hội học đến kinh tế, việc hiểu rõ sự phân tán của dữ liệu là nền tảng. Độ lệch chuẩn giúp nhà nghiên cứu đánh giá mức độ biến động của các biến số. Một độ lệch chuẩn thấp thường cho thấy dữ liệu khá nhất quán, kết quả thu được có thể đại diện tốt cho tổng thể. Ngược lại, độ lệch chuẩn cao báo hiệu sự đa dạng hoặc biến động lớn trong dữ liệu, điều này có thể cần được giải thích thêm hoặc xem xét các yếu tố ảnh hưởng khác.
Các phần mềm thống kê chuyên dụng phục vụ nghiên cứu như SPSS luôn hiển thị độ lệch chuẩn như một chỉ số mặc định khi bạn yêu cầu thống kê mô tả. Điều này nhấn mạnh tầm quan trọng của nó như một công cụ cơ bản nhưng hiệu quả để tóm tắt đặc điểm của tập dữ liệu, giúp nhà nghiên cứu có cái nhìn ban đầu sâu sắc hơn trước khi tiến hành các phân tích phức tạp. Nó giúp bạn không chỉ biết "trung bình là bao nhiêu" mà còn biết "dữ liệu xung quanh trung bình đó như thế nào".
Độ lệch chuẩn Đo lường rủi ro đầu tư
Trong thế giới đầu tư đầy sóng gió, rủi ro luôn là một yếu tố khiến các nhà đầu tư phải đau đầu suy nghĩ. Làm sao để biết một cổ phiếu, một quỹ đầu tư hay cả danh mục của mình "chao đảo" đến mức nào? Đây chính là lúc độ lệch chuẩn phát huy vai trò cực kỳ quan trọng của nó.
Hãy xem độ lệch chuẩn như một thước đo biến động. Trong tài chính, biến động thường được xem là đồng nghĩa với rủi ro. Nếu giá của một tài sản (như cổ phiếu) hay lợi nhuận của một quỹ liên tục nhảy múa, lúc tăng vọt, lúc giảm sâu, thì độ lệch chuẩn của nó sẽ cao. Điều này báo hiệu mức độ rủi ro lớn hơn, vì bạn khó lòng đoán trước được giá trị của nó sẽ đi về đâu trong tương lai gần. Ngược lại, một tài sản có giá trị hoặc lợi nhuận tương đối ổn định, ít biến động, sẽ có độ lệch chuẩn thấp hơn, đồng nghĩa với rủi ro thấp hơn.
Các nhà đầu tư chuyên nghiệp lẫn cá nhân đều dùng độ lệch chuẩn để "cân đo đong đếm" rủi ro này. Khi đứng trước hai lựa chọn đầu tư mang lại lợi nhuận kỳ vọng tương đương nhau, người ta thường có xu hướng chọn cái nào có độ lệch chuẩn thấp hơn, bởi vì nó ít rủi ro hơn, "yên tâm" hơn.
Độ lệch chuẩn không chỉ giúp đánh giá rủi ro của từng tài sản riêng lẻ mà còn cực kỳ hữu ích khi xem xét cả một danh mục đầu tư. Bằng cách kết hợp các tài sản có đặc điểm biến động khác nhau, nhà đầu tư có thể xây dựng một danh mục có độ lệch chuẩn (tức rủi ro tổng thể) thấp hơn so với việc chỉ nắm giữ một loại tài sản duy nhất. Đây chính là nguyên tắc cốt lõi của đa dạng hóa.
Tóm lại, trong phân tích tài chính và đầu tư, độ lệch chuẩn là công cụ không thể thiếu giúp chúng ta lượng hóa và hiểu rõ hơn về sự bất ổn, hay còn gọi là rủi ro. Nó là kim chỉ nam giúp nhà đầu tư đưa ra quyết định sáng suốt, phù hợp với khẩu vị rủi ro của bản thân.
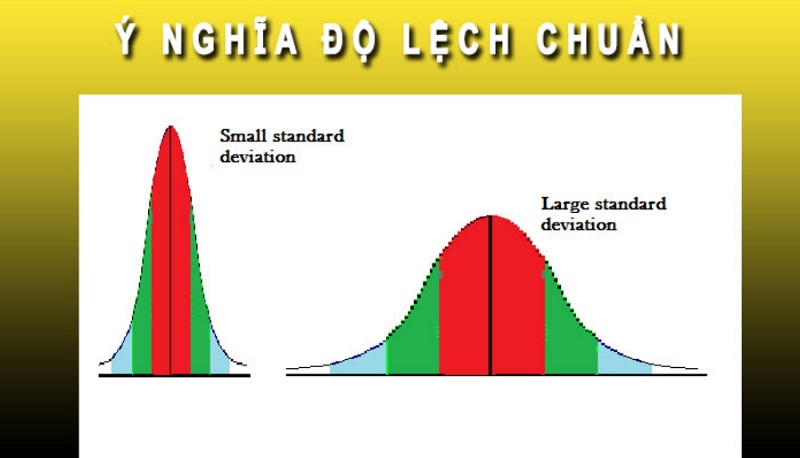
Hiểu đúng về độ lệch chuẩn
Nhiều người khi mới làm quen với thống kê thường băn khoăn: "Độ lệch chuẩn bao nhiêu thì được coi là tốt?". Thật ra, không có con số "chuẩn" nào cho độ lệch chuẩn cả, giống như hỏi "bao nhiêu tiền là đủ?" vậy đó. Mức độ "tốt" hay "chưa tốt" của độ lệch chuẩn hoàn toàn phụ thuộc vào ngữ cảnh bạn đang xem xét và mục tiêu phân tích của bạn là gì.
Hãy hình dung thế này: nếu bạn đo chiều cao của học sinh trong một lớp (dữ liệu khá tập trung), bạn sẽ mong đợi độ lệch chuẩn nhỏ. Một độ lệch chuẩn lớn ở đây có thể báo hiệu điều gì đó bất thường. Ngược lại, nếu bạn khảo sát thu nhập hàng năm của người dân trên cả nước (dữ liệu rất phân tán), độ lệch chuẩn chắc chắn sẽ rất lớn, và đó là điều bình thường. Một độ lệch chuẩn nhỏ trong trường hợp này lại mới là lạ!
Vì thế, thay vì cố tìm một con số "đẹp", hãy so sánh độ lệch chuẩn với giá trị trung bình của chính tập dữ liệu đó, hoặc so sánh độ lệch chuẩn của tập dữ liệu này với tập dữ liệu khác có cùng bản chất.
Để việc so sánh trở nên ý nghĩa hơn, người ta thường dùng đến một "trợ thủ" đắc lực gọi là Hệ số biến thiên (Coefficient of Variation – CV). Hệ số này tính bằng cách lấy độ lệch chuẩn chia cho giá trị trung bình (và thường nhân với 100% để dễ đọc). CV giúp bạn thấy rõ mức độ biến động tương đối của dữ liệu so với giá trị trung bình của nó. Nhờ CV, bạn có thể so sánh độ biến động của hai tập dữ liệu có đơn vị đo hoặc giá trị trung bình khác xa nhau, ví dụ như so sánh sự biến động giá của một cổ phiếu giá thấp và một cổ phiếu giá cao.
Tuy mạnh mẽ, độ lệch chuẩn cũng có "điểm yếu" đấy nhé. Nó rất nhạy cảm với các giá trị "lạc loài" (outliers) trong dữ liệu. Chỉ cần vài con số quá lớn hoặc quá nhỏ so với phần còn lại, độ lệch chuẩn có thể bị "kéo" theo đáng kể, làm sai lệch cách nhìn nhận về sự phân tán chung. Hơn nữa, độ lệch chuẩn chỉ cho bạn biết mức độ phân tán xung quanh giá trị trung bình, chứ không nói lên hình dạng phân phối của dữ liệu (nó có đối xứng không, có bị lệch về một phía không, hay có nhiều "đỉnh" không).
Vì vậy, khi dùng độ lệch chuẩn, đừng chỉ nhìn mỗi con số. Hãy luôn kết hợp nó với các thống kê mô tả khác như giá trị trung bình, trung vị, khoảng tứ phân vị, và đặc biệt là các biểu đồ trực quan như biểu đồ tần số (histogram) hay biểu đồ hộp (box plot). Chỉ khi nhìn bức tranh toàn cảnh, bạn mới có thể hiểu đúng và sử dụng hiệu quả "thước đo biến động" quan trọng này.